 |
Looping est un logiciel d'édition de modèles conceptuels de bases de données. Léger (< 5Mo) il permet cependant de nombreuses fonctionnalités.
|
1 mai 2019
10 avril 2019
Algorithme de parcours en largeur

|
L'algorithme de parcours en largeur commence à un nœud quelconque d’un graphe, parfois appelé "clé de recherche", et explore tous les nœuds voisins de même profondeur avant de passer aux nœuds situés au prochain niveau de profondeur. On pourrait le comparer à une "onde".
|

|

|
Si nous changeons le mode de gestion de la liste de FIFO à LIFO, alors nous transformons notre algorithme de parcours en largeur en algorithme de parcours en profondeur. (sans récursivité)
|
Si on doit vérifier qu'une connexion existe entre deux nœuds, alors l'algorithme de parcours en profondeur sera, en moyenne, plus performant. En revanche, si nous recherchons le plus court chemin, et si les nœuds sont équidistants alors l'algorithme de parcours en largeur sera meilleur. En effet, avec l'algorithme de parcours en profondeur, lorsque l'on tombe sur l'élément recherché, il peut exister un autre chemin plus court. Ce qui implique que l'ensemble des nœuds de l'arbre doit être parcouru.
L'algorithme de Dijkstra est une généralisation du parcours en largeur prenant en compte une pondération entre les nœuds (distance par exemple).
9 avril 2019
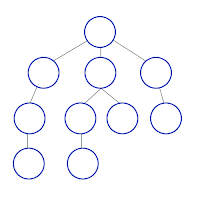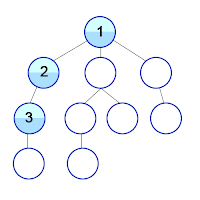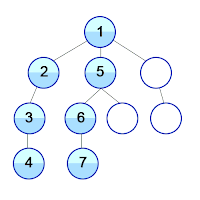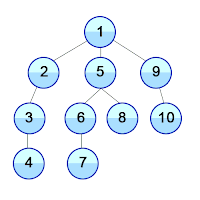
Algorithme de parcours en profondeur
|
L'algorithme de parcours en profondeur correspond à la méthode intuitive qu'on utilise pour trouver la sortie d'un labyrinthe. En effet, il suffit de toujours longer le mur pour trouver la sortie. (labyrinthe parfait)
|
Un algorithme qui contient un ou des appels à lui-même est dit récursif. Ce procédé est souvent employé dans la conception d'algorithmes basée sur le paradigme diviser pour régner.
Voici un exemple de récursivité avec une fonction de puissance.
|

|

|
Attention à ne pas dépasser la taille de la pile des exécutions (Sauvegarde des appels de fonctions). En électronique embarquée, la récursivité est souvent proscrite ! L'utilisation de la pile restant trop imprévisible.
|
5 avril 2019
SVG Minifier

|
Les éditeurs graphiques vectoriels tels qu'Adobe Illustrator ou Inkscape incorporent de nombreuses informations dans un fichier SVG qui ne sont pas requises pour la présentation.
SVG Minifier supprime ces informations superflues, réduisant ainsi la taille de vos fichiers SVG.
|
Algorithme de Boruvka (1926)
L'Algorithme de Borůvka a été publié pour la première fois en 1926 par Otakar Borůvka en tant que méthode de construction d’un réseau d’électricité efficace pour la Moravie.
| 1️⃣️ |
On parcours chaque points en gardant la branche de poids faible (la plus petite valeur).
|
| 2️⃣️ |
On forme des groupes (points reliées entres eux) et on les relies avec la branche de poids faible.
|
En algorithmique, on parle de chercher un "arbre couvrant minimum".
Algorithmes similaires : Algorithme de Kruskal - Algorithme de Prim.
25 mars 2019
Écran Sphérique - Étude - Fréquences des Rafraîchissements des LEDs
Suivant la position des LEDs RGB sur l'arc, leurs fréquences de rafraîchissement diffèrent. Plus on se rapproche de l'équateur, et plus le besoin des actualisations augmente. Afin de déterminer le nombre de pixels nécessaires sur l'axe horizontal, nous déterminons d'abord l'angle ϑ formé par la droite passant par l'origine et le pôle Nord, et celle passant par l'origine et notre pixel (position verticale voulue).

Comme nous sommes sur une sphère, n'importe quelle longueur de méridien (Arc) équivaut à la moitié de la longueur de l'équateur. Donc, en multipliant le sinus de l'angle, par le double du nombre total de pixels sur l'arc ( -1 car on garde un seul pôle), on détermine le nombre total nécessaire sur l'axe horizontal.

Le tableau suivant regroupe les calculs afin de déterminer le nombre de rafraîchissements de chacune des LEDs RGB suivant leur position et ainsi, connaitre le nombre total des pixels de l'écran.
|

|
| LED V | ϑ | Sin | LED H | ≈ | Err | Rcy | ||
|---|---|---|---|---|---|---|---|---|
| Pôle Nord | 1 | 0,0 | 0,000 | 1,00 | 1 | 1,00 | 0,25% | |
| 2 | 0,9 | 0,016 | 6,28 | 6 | 0,95 | 1,50% | ||
| 3 | 1,8 | 0,031 | 12,56 | 13 | 1,03 | 3,25% | ||
| 4 | 2,7 | 0,047 | 18,84 | 19 | 1,01 | 4,75% | ||
| 5 | 3,6 | 0,063 | 25,12 | 25 | 1,00 | 6,25% | ||
| 6 | 4,5 | 0,078 | 31,38 | 31 | 0,99 | 7,75% | ||
| 7 | 5,4 | 0,094 | 37,64 | 38 | 1,01 | 9,50% | ||
| 8 | 6,3 | 0,110 | 43,89 | 44 | 1,00 | 11,00% | ||
| 9 | 7,2 | 0,125 | 50,13 | 50 | 1,00 | 12,50% | ||
| 10 | 8,1 | 0,141 | 56,36 | 56 | 0,99 | 14,00% | ||
| 11 | 9,0 | 0,156 | 62,57 | 63 | 1,01 | 15,75% | ||
| 12 | 9,9 | 0,172 | 68,77 | 69 | 1,00 | 17,25% | ||
| 13 | 10,8 | 0,187 | 74,95 | 75 | 1,00 | 18,75% | ||
| 14 | 11,7 | 0,203 | 81,11 | 81 | 1,00 | 20,25% | ||
| 15 | 12,6 | 0,218 | 87,26 | 87 | 1,00 | 21,75% | ||
| 16 | 13,5 | 0,233 | 93,38 | 93 | 1,00 | 23,25% | ||
| 17 | 14,4 | 0,249 | 99,48 | 99 | 1,00 | 24,75% | ||
| 18 | 15,3 | 0,264 | 105,55 | 106 | 1,00 | 26,50% | ||
| 19 | 16,2 | 0,279 | 111,60 | 112 | 1,00 | 28,00% | ||
| 20 | 17,1 | 0,294 | 117,62 | 118 | 1,00 | 29,50% | ||
| 21 | 18,0 | 0,309 | 123,61 | 124 | 1,00 | 31,00% | ||
| 22 | 18,9 | 0,324 | 129,57 | 130 | 1,00 | 32,50% | ||
| 23 | 19,8 | 0,339 | 135,50 | 135 | 1,00 | 33,75% | ||
| 24 | 20,7 | 0,353 | 141,39 | 141 | 1,00 | 35,25% | ||
| 25 | 21,6 | 0,368 | 147,25 | 147 | 1,00 | 36,75% | ||
| 26 | 22,5 | 0,383 | 153,07 | 153 | 1,00 | 38,25% | ||
| 27 | 23,4 | 0,397 | 158,86 | 159 | 1,00 | 39,75% | ||
| 28 | 24,3 | 0,412 | 164,61 | 165 | 1,00 | 41,25% | ||
| 29 | 25,2 | 0,426 | 170,31 | 170 | 1,00 | 42,50% | ||
| 30 | 26,1 | 0,440 | 175,98 | 176 | 1,00 | 44,00% | ||
| 31 | 27,0 | 0,454 | 181,60 | 182 | 1,00 | 45,50% | ||
| 32 | 27,9 | 0,468 | 187,17 | 187 | 1,00 | 46,75% | ||
| 33 | 28,8 | 0,482 | 192,70 | 193 | 1,00 | 48,25% | ||
| 34 | 29,7 | 0,495 | 198,18 | 198 | 1,00 | 49,50% | ||
| 35 | 30,6 | 0,509 | 203,62 | 204 | 1,00 | 51,00% | ||
| 36 | 31,5 | 0,522 | 209,00 | 209 | 1,00 | 52,25% | ||
| 37 | 32,4 | 0,536 | 214,33 | 214 | 1,00 | 53,50% | ||
| 38 | 33,3 | 0,549 | 219,61 | 220 | 1,00 | 55,00% | ||
| 39 | 34,2 | 0,562 | 224,83 | 225 | 1,00 | 56,25% | ||
| 40 | 35,1 | 0,575 | 230,00 | 230 | 1,00 | 57,50% | ||
| 41 | 36,0 | 0,588 | 235,11 | 235 | 1,00 | 58,75% | ||
| 42 | 36,9 | 0,600 | 240,17 | 240 | 1,00 | 60,00% | ||
| 43 | 37,8 | 0,613 | 245,16 | 245 | 1,00 | 61,25% | ||
| 44 | 38,7 | 0,625 | 250,10 | 250 | 1,00 | 62,50% | ||
| 45 | 39,6 | 0,637 | 254,97 | 255 | 1,00 | 63,75% | ||
| 46 | 40,5 | 0,649 | 259,78 | 260 | 1,00 | 65,00% | ||
| 47 | 41,4 | 0,661 | 264,52 | 265 | 1,00 | 66,25% | ||
| 48 | 42,3 | 0,673 | 269,21 | 269 | 1,00 | 67,25% | ||
| 49 | 43,2 | 0,685 | 273,82 | 274 | 1,00 | 68,50% | ||
| 50 | 44,1 | 0,696 | 278,37 | 278 | 1,00 | 69,50% | ||
| 51 | 45,0 | 0,707 | 282,84 | 283 | 1,00 | 70,75% | ||
| 52 | 45,9 | 0,718 | 287,25 | 287 | 1,00 | 71,75% | ||
| 53 | 46,8 | 0,729 | 291,59 | 292 | 1,00 | 73,00% | ||
| 54 | 47,7 | 0,740 | 295,85 | 296 | 1,00 | 74,00% | ||
| 55 | 48,6 | 0,750 | 300,04 | 300 | 1,00 | 75,00% | ||
| 56 | 49,5 | 0,760 | 304,16 | 304 | 1,00 | 76,00% | ||
| 57 | 50,4 | 0,771 | 308,21 | 308 | 1,00 | 77,00% | ||
| 58 | 51,3 | 0,780 | 312,17 | 312 | 1,00 | 78,00% | ||
| 59 | 52,2 | 0,790 | 316,06 | 316 | 1,00 | 79,00% | ||
| 60 | 53,1 | 0,800 | 319,87 | 320 | 1,00 | 80,00% | ||
| 61 | 54,0 | 0,809 | 323,61 | 324 | 1,00 | 81,00% | ||
| 62 | 54,9 | 0,818 | 327,26 | 327 | 1,00 | 81,75% | ||
| 63 | 55,8 | 0,827 | 330,83 | 331 | 1,00 | 82,75% | ||
| 64 | 56,7 | 0,836 | 334,32 | 334 | 1,00 | 83,50% | ||
| 65 | 57,6 | 0,844 | 337,73 | 338 | 1,00 | 84,50% | ||
| 66 | 58,5 | 0,853 | 341,06 | 341 | 1,00 | 85,25% | ||
| 67 | 59,4 | 0,861 | 344,30 | 344 | 1,00 | 86,00% | ||
| 68 | 60,3 | 0,869 | 347,45 | 347 | 1,00 | 86,75% | ||
| 69 | 61,2 | 0,876 | 350,52 | 351 | 1,00 | 87,75% | ||
| 70 | 62,1 | 0,884 | 353,51 | 354 | 1,00 | 88,50% | ||
| 71 | 63,0 | 0,891 | 356,40 | 356 | 1,00 | 89,00% | ||
| 72 | 63,9 | 0,898 | 359,21 | 359 | 1,00 | 89,75% | ||
| 73 | 64,8 | 0,905 | 361,93 | 362 | 1,00 | 90,50% | ||
| 74 | 65,7 | 0,911 | 364,56 | 365 | 1,00 | 91,25% | ||
| Cancer | 75 | 66,6 | 0,918 | 367,10 | 367 | 1,00 | 91,75% | |
| 76 | 67,5 | 0,924 | 369,55 | 370 | 1,00 | 92,50% | ||
| 77 | 68,4 | 0,930 | 371,91 | 372 | 1,00 | 93,00% | ||
| 78 | 69,3 | 0,935 | 374,18 | 374 | 1,00 | 93,50% | ||
| 79 | 70,2 | 0,941 | 376,35 | 376 | 1,00 | 94,00% | ||
| 80 | 71,1 | 0,946 | 378,43 | 378 | 1,00 | 94,50% | ||
| 81 | 72,0 | 0,951 | 380,42 | 380 | 1,00 | 95,00% | ||
| 82 | 72,9 | 0,956 | 382,32 | 382 | 1,00 | 95,50% | ||
| 83 | 73,8 | 0,960 | 384,12 | 384 | 1,00 | 96,00% | ||
| 84 | 74,7 | 0,965 | 385,82 | 386 | 1,00 | 96,50% | ||
| 85 | 75,6 | 0,969 | 387,43 | 387 | 1,00 | 96,75% | ||
| 86 | 76,5 | 0,972 | 388,95 | 389 | 1,00 | 97,25% | ||
| 87 | 77,4 | 0,976 | 390,37 | 390 | 1,00 | 97,50% | ||
| 88 | 78,3 | 0,979 | 391,69 | 392 | 1,00 | 98,00% | ||
| 89 | 79,2 | 0,982 | 392,91 | 393 | 1,00 | 98,25% | ||
| 90 | 80,1 | 0,985 | 394,04 | 394 | 1,00 | 98,50% | ||
| 91 | 81,0 | 0,988 | 395,08 | 395 | 1,00 | 98,75% | ||
| 92 | 81,9 | 0,990 | 396,01 | 396 | 1,00 | 99,00% | ||
| 93 | 82,8 | 0,992 | 396,85 | 397 | 1,00 | 99,25% | ||
| 94 | 83,7 | 0,994 | 397,58 | 398 | 1,00 | 99,50% | ||
| 95 | 84,6 | 0,996 | 398,22 | 398 | 1,00 | 99,50% | ||
| 96 | 85,5 | 0,997 | 398,77 | 399 | 1,00 | 99,75% | ||
| 97 | 86,4 | 0,998 | 399,21 | 399 | 1,00 | 99,75% | ||
| 98 | 87,3 | 0,999 | 399,56 | 400 | 1,00 | 100,00% | ||
| 99 | 88,2 | 1,000 | 399,80 | 400 | 1,00 | 100,00% | ||
| 100 | 89,1 | 1,000 | 399,95 | 400 | 1,00 | 100,00% | ||
| Equateur | 101 | 90,0 | 1,000 | 400,00 | 400 | 1,00 | 100,00% | |
| 102 | 90,9 | 1,000 | 399,95 | 400 | 1,00 | 100,00% | ||
| 103 | 91,8 | 1,000 | 399,80 | 400 | 1,00 | 100,00% | ||
| 104 | 92,7 | 0,999 | 399,56 | 400 | 1,00 | 100,00% | ||
| 105 | 93,6 | 0,998 | 399,21 | 399 | 1,00 | 99,75% | ||
| 106 | 94,5 | 0,997 | 398,77 | 399 | 1,00 | 99,75% | ||
| 107 | 95,4 | 0,996 | 398,22 | 398 | 1,00 | 99,50% | ||
| 108 | 96,3 | 0,994 | 397,58 | 398 | 1,00 | 99,50% | ||
| 109 | 97,2 | 0,992 | 396,85 | 397 | 1,00 | 99,25% | ||
| 110 | 98,1 | 0,990 | 396,01 | 396 | 1,00 | 99,00% | ||
| 111 | 99,0 | 0,988 | 395,08 | 395 | 1,00 | 98,75% | ||
| 112 | 99,9 | 0,985 | 394,04 | 394 | 1,00 | 98,50% | ||
| 113 | 100,8 | 0,982 | 392,91 | 393 | 1,00 | 98,25% | ||
| 114 | 101,7 | 0,979 | 391,69 | 392 | 1,00 | 98,00% | ||
| 115 | 102,6 | 0,976 | 390,37 | 390 | 1,00 | 97,50% | ||
| 116 | 103,5 | 0,972 | 388,95 | 389 | 1,00 | 97,25% | ||
| 117 | 104,4 | 0,969 | 387,43 | 387 | 1,00 | 96,75% | ||
| 118 | 105,3 | 0,965 | 385,82 | 386 | 1,00 | 96,50% | ||
| 119 | 106,2 | 0,960 | 384,12 | 384 | 1,00 | 96,00% | ||
| 120 | 107,1 | 0,956 | 382,32 | 382 | 1,00 | 95,50% | ||
| 121 | 108,0 | 0,951 | 380,42 | 380 | 1,00 | 95,00% | ||
| 122 | 108,9 | 0,946 | 378,43 | 378 | 1,00 | 94,50% | ||
| 123 | 109,8 | 0,941 | 376,35 | 376 | 1,00 | 94,00% | ||
| 124 | 110,7 | 0,935 | 374,18 | 374 | 1,00 | 93,50% | ||
| 125 | 111,6 | 0,930 | 371,91 | 372 | 1,00 | 93,00% | ||
| 126 | 112,5 | 0,924 | 369,55 | 370 | 1,00 | 92,50% | ||
| Capricorne | 127 | 113,4 | 0,918 | 367,10 | 367 | 1,00 | 91,75% | |
| 128 | 114,3 | 0,911 | 364,56 | 365 | 1,00 | 91,25% | ||
| 129 | 115,2 | 0,905 | 361,93 | 362 | 1,00 | 90,50% | ||
| 130 | 116,1 | 0,898 | 359,21 | 359 | 1,00 | 89,75% | ||
| 131 | 117,0 | 0,891 | 356,40 | 356 | 1,00 | 89,00% | ||
| 132 | 117,9 | 0,884 | 353,51 | 354 | 1,00 | 88,50% | ||
| 133 | 118,8 | 0,876 | 350,52 | 351 | 1,00 | 87,75% | ||
| 134 | 119,7 | 0,869 | 347,45 | 347 | 1,00 | 86,75% | ||
| 135 | 120,6 | 0,861 | 344,30 | 344 | 1,00 | 86,00% | ||
| 136 | 121,5 | 0,853 | 341,06 | 341 | 1,00 | 85,25% | ||
| 137 | 122,4 | 0,844 | 337,73 | 338 | 1,00 | 84,50% | ||
| 138 | 123,3 | 0,836 | 334,32 | 334 | 1,00 | 83,50% | ||
| 139 | 124,2 | 0,827 | 330,83 | 331 | 1,00 | 82,75% | ||
| 140 | 125,1 | 0,818 | 327,26 | 327 | 1,00 | 81,75% | ||
| 141 | 126,0 | 0,809 | 323,61 | 324 | 1,00 | 81,00% | ||
| 142 | 126,9 | 0,800 | 319,87 | 320 | 1,00 | 80,00% | ||
| 143 | 127,8 | 0,790 | 316,06 | 316 | 1,00 | 79,00% | ||
| 144 | 128,7 | 0,780 | 312,17 | 312 | 1,00 | 78,00% | ||
| 145 | 129,6 | 0,771 | 308,21 | 308 | 1,00 | 77,00% | ||
| 146 | 130,5 | 0,760 | 304,16 | 304 | 1,00 | 76,00% | ||
| 147 | 131,4 | 0,750 | 300,04 | 300 | 1,00 | 75,00% | ||
| 148 | 132,3 | 0,740 | 295,85 | 296 | 1,00 | 74,00% | ||
| 149 | 133,2 | 0,729 | 291,59 | 292 | 1,00 | 73,00% | ||
| 150 | 134,1 | 0,718 | 287,25 | 287 | 1,00 | 71,75% | ||
| 151 | 135,0 | 0,707 | 282,84 | 283 | 1,00 | 70,75% | ||
| 152 | 135,9 | 0,696 | 278,37 | 278 | 1,00 | 69,50% | ||
| 153 | 136,8 | 0,685 | 273,82 | 274 | 1,00 | 68,50% | ||
| 154 | 137,7 | 0,673 | 269,21 | 269 | 1,00 | 67,25% | ||
| 155 | 138,6 | 0,661 | 264,52 | 265 | 1,00 | 66,25% | ||
| 156 | 139,5 | 0,649 | 259,78 | 260 | 1,00 | 65,00% | ||
| 157 | 140,4 | 0,637 | 254,97 | 255 | 1,00 | 63,75% | ||
| 158 | 141,3 | 0,625 | 250,10 | 250 | 1,00 | 62,50% | ||
| 159 | 142,2 | 0,613 | 245,16 | 245 | 1,00 | 61,25% | ||
| 160 | 143,1 | 0,600 | 240,17 | 240 | 1,00 | 60,00% | ||
| 161 | 144,0 | 0,588 | 235,11 | 235 | 1,00 | 58,75% | ||
| 162 | 144,9 | 0,575 | 230,00 | 230 | 1,00 | 57,50% | ||
| 163 | 145,8 | 0,562 | 224,83 | 225 | 1,00 | 56,25% | ||
| 164 | 146,7 | 0,549 | 219,61 | 220 | 1,00 | 55,00% | ||
| 165 | 147,6 | 0,536 | 214,33 | 214 | 1,00 | 53,50% | ||
| 166 | 148,5 | 0,522 | 209,00 | 209 | 1,00 | 52,25% | ||
| 167 | 149,4 | 0,509 | 203,62 | 204 | 1,00 | 51,00% | ||
| 168 | 150,3 | 0,495 | 198,18 | 198 | 1,00 | 49,50% | ||
| 169 | 151,2 | 0,482 | 192,70 | 193 | 1,00 | 48,25% | ||
| 170 | 152,1 | 0,468 | 187,17 | 187 | 1,00 | 46,75% | ||
| 171 | 153,0 | 0,454 | 181,60 | 182 | 1,00 | 45,50% | ||
| 172 | 153,9 | 0,440 | 175,98 | 176 | 1,00 | 44,00% | ||
| 173 | 154,8 | 0,426 | 170,31 | 170 | 1,00 | 42,50% | ||
| 174 | 155,7 | 0,412 | 164,61 | 165 | 1,00 | 41,25% | ||
| 175 | 156,6 | 0,397 | 158,86 | 159 | 1,00 | 39,75% | ||
| 176 | 157,5 | 0,383 | 153,07 | 153 | 1,00 | 38,25% | ||
| 177 | 158,4 | 0,368 | 147,25 | 147 | 1,00 | 36,75% | ||
| 178 | 159,3 | 0,353 | 141,39 | 141 | 1,00 | 35,25% | ||
| 179 | 160,2 | 0,339 | 135,50 | 135 | 1,00 | 33,75% | ||
| 180 | 161,1 | 0,324 | 129,57 | 130 | 1,00 | 32,50% | ||
| 181 | 162,0 | 0,309 | 123,61 | 124 | 1,00 | 31,00% | ||
| 182 | 162,9 | 0,294 | 117,62 | 118 | 1,00 | 29,50% | ||
| 183 | 163,8 | 0,279 | 111,60 | 112 | 1,00 | 28,00% | ||
| 184 | 164,7 | 0,264 | 105,55 | 106 | 1,00 | 26,50% | ||
| 185 | 165,6 | 0,249 | 99,48 | 99 | 1,00 | 24,75% | ||
| 186 | 166,5 | 0,233 | 93,38 | 93 | 1,00 | 23,25% | ||
| 187 | 167,4 | 0,218 | 87,26 | 87 | 1,00 | 21,75% | ||
| 188 | 168,3 | 0,203 | 81,11 | 81 | 1,00 | 20,25% | ||
| 189 | 169,2 | 0,187 | 74,95 | 75 | 1,00 | 18,75% | ||
| 190 | 170,1 | 0,172 | 68,77 | 69 | 1,00 | 17,25% | ||
| 191 | 171,0 | 0,156 | 62,57 | 63 | 1,01 | 15,75% | ||
| 192 | 171,9 | 0,141 | 56,36 | 56 | 0,99 | 14,00% | ||
| 193 | 172,8 | 0,125 | 50,13 | 50 | 1,00 | 12,50% | ||
| 194 | 173,7 | 0,110 | 43,89 | 44 | 1,00 | 11,00% | ||
| 195 | 174,6 | 0,094 | 37,64 | 38 | 1,01 | 9,50% | ||
| 196 | 175,5 | 0,078 | 31,38 | 31 | 0,99 | 7,75% | ||
| 197 | 176,4 | 0,063 | 25,12 | 25 | 1,00 | 6,25% | ||
| 198 | 177,3 | 0,047 | 18,84 | 19 | 1,01 | 4,75% | ||
| 199 | 178,2 | 0,031 | 12,56 | 13 | 1,03 | 3,25% | ||
| 200 | 179,1 | 0,016 | 6,28 | 6 | 0,95 | 1,50% | ||
| Pôle Sud | 201 | 180,0 | 0,000 | 1,00 | 1 | 1,00 | 0,25% |

|
"Avec la formule, LED_V(1) "et "LED_V(201)" valent normalement "0". Mais nous ajoutons tout de même une LED afin d'afficher les pôles.
|
Pour un tour complet, les LEDs des pôles n'affichent qu'un seul pixel, et celles au niveau de l'équateur en affichent 400. Cela aura un impacte sur la luminosité globale de l'écran sphérique. Il nous faut pour cela trouver des LEDs RGB avec une forte luminosité.
Les LEDs qui devront afficher le plus grand nombre de pixels, seront aussi celles qui auront leur vitesse de déplacement élevée. Ainsi, en essayant d'optimiser la ventilation (forme mécanique), nous pourrons les "suralimenter".
|

|

|
En décomposant le nombre d'actualisations suivant la position de la LED sur l'arc, on peut représenter l'écran sphérique en deux dimensions. Chacun des carrés représente un pixel (400 × 201 pixels). Cette représentation est appelée Projection Sinusoïdale.
|
Pour un écran sphérique de résolution 400 ⨉ 201, nous avons un total de 50932 pixels. Pour passer d'une image rectangulaire à une projection sinusoïdale, nous perdons 36.65% des pixels originaux.
|
24 mars 2019
Algorithme de Prim (1930)

|
L'Algorithme de Prim a été développé en 1930 par le mathématicien tchèque Vojtech Jarnik puis a été redécouvert et republié par Robert C. Prim et Edsger W. Dijkstra en 1959. Il consiste à trouver l'arbre couvrant minimum.
Imaginez que vous devez relier plusieurs villes en électricité, câble téléphonique ou chemins de fer. Quelle solution me donne une distance totale minimum ?? (distance minimum ≈ argent minimum)
La recherche du point le plus proche est la fonction cruciale de cet algorithme. D'elle, dépend la performance globale.
Algorithmes similaires : Algorithme de Borůvka - Algorithme de Kruskal. |
23 mars 2019
Écran Sphérique - Étude - Diamètre de l'Arc
Il existe de nombreuses références pour les LEDs. Leur forme peut varier mais également leur diamètre. Ainsi, ce paramètre, mais également le nombre, impactent sur la longueur de l'arc.
|
Le tableau indique le diamètre de l'arc suivant le diamètre de la LED et le nombre utilisé.
 

|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Souhaitant avoir 201 LEDs sur l'arc, les diamètres à partir de 5 mm sont à éviter. En effet, le diamètre devient trop conséquent et les contraintes mécaniques avec. Je pense m'orienter vers des LEDs entre 3 mm et 3.5 mm. Ce qui me donnerait un diamètre entre 382 mm et 445,6 mm.
15 mars 2019
Écran Sphérique - Étude - Modulation Binaire
Une autre méthode que le PWM (vue dans la précédente publication), rarement vue (hormis de par la personne qui me l'a enseigné que je salue au passage) et pourtant bien plus performante, la Modulation Binaire - Binary Modulation. Elle se révèle vraiment efficace surtout lorsqu’il s’agit de contrôler un grand nombre de sorties avec un fort échantillonnage (résolution).
 |
À chaque cycles, on compare le nombre de cycles enregistrés dans la variable "Cycle" à la constante "CycleMax" dépendant à l'échantillonnage désiré. Pour n = 4 bits, nous aurons CycleMax = n = 4. Si "Cycle" est supérieur ou égal, on le réinitialise à 0. Puis on applique, à la sortie "Out", l’état du bit de la variable "Value" indexé par le compteur "Cycle".


|
La variable "Period", correspondant à la période du prochain cycle, est le résultat de "IntialPeriod" multiplié par 2 à la puissance "Cycle". Enfin, on incrémente le compteur "Cycle".
|
Notre rapport cyclique "Rcy" est bien modulé en conséquence par la variable "Value".
 La Modulation Binaire permet un gain (traitement global et/ou énergie) non négligeable que ce soit sur un microcontrôleur ou un FPGA. |
|
|||||||||||||||||||||||||||||||||||||||||||||||

|
Remarque : Pourquoi partir du bit de poids faible plutôt que celui de poids fort ?
Car en partant du bit de poids faible, nous passons par la multiplication (décalage des bits vers la gauche) plutôt que la division. Et nous nous abstenons, ainsi, d'une éventuelle division par 2 d'un nombre impaire (Si le calcul de "InitialPeriod" était mauvais). Cependant, si le nombre de sorties est vraiment conséquent et l'échantillonnage élevé, afin de mieux répartir la charge globale sur le temps, nous pouvons diviser équitablement les sorties en deux listes. Chacune partant du bit de poids opposé. Ainsi, on évite la charge "brusque" demandée lors des cycles à faible période. |
Inscription à :
Commentaires (Atom)






