Algorithme de parcours en largeur

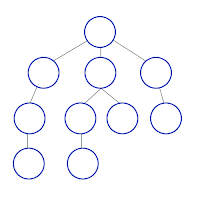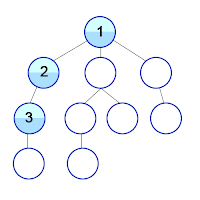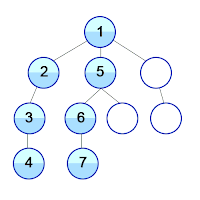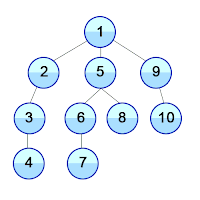
L'algorithme de parcours en largeur commence à un nœud quelconque d’un graphe, parfois appelé "clé de recherche", et explore tous les nœuds voisins de même profondeur avant de passer aux nœuds situés au prochain niveau de profondeur. On pourrait le comparer à une "onde". 1️⃣️ On retire le premier élément entré dans notre liste de nœuds à explorer (FIFO) et on le traite. (Seulement la clé de recherche s'y trouve au démarrage) 2️⃣️ On indique que le nœud a été exploré, puis on ajoute, à la fin de notre liste de nœuds à explorer, tous les nœuds enfants non explorés. 3️⃣️ Si la liste à explorer n'est pas vide et que les conditions de fin ne sont pas remplies (élément recherché non trouvé par exemple), on répète l'étape 1.

Une pile est une liste avec gestion LIFO (Last In, First Out - Dernier entré, premier sortie), une file est une liste avec gestion FIFO (First In, First Out - Premier entré, premier sortie).

Si nous changeons le mode de gestion de la liste de FIFO à LIFO, alors nous transformons notre algorithme de parcours en largeur en algorithme de parcours en profondeur. (sans récursivité)

Si on doit vérifier qu'une connexion existe entre deux nœuds, alors l'algorithme de parcours en profondeur sera, en moyenne, plus performant. En revanche, si nous recherchons le plus court chemin, et si les nœuds sont équidistants alors l'algorithme de parcours en largeur sera meilleur. En effet, avec l'algorithme de parcours en profondeur, lorsque l'on tombe sur l'élément recherché, il peut exister un autre chemin plus court. Ce qui implique que l'ensemble des nœuds de l'arbre doit être parcouru.

L'algorithme de Dijkstra est une généralisation du parcours en largeur prenant en compte une pondération entre les nœuds (distance par exemple).

Algorithme de parcours en profondeur

L'algorithme de parcours en profondeur correspond à la méthode intuitive qu'on utilise pour trouver la sortie d'un labyrinthe. En effet, il suffit de toujours longer le mur pour trouver la sortie. (labyrinthe parfait) 1️⃣️ On indique que le nœud a été exploré. 2️⃣️ On arrête si nous sommes sur le nœud recherché. (non obligatoire) 3️⃣️ On répète la procédure par récursivité pour tous les enfants du nœud non explorés.

---

Un algorithme qui contient un ou des appels à lui-même est dit récursif. Ce procédé est souvent employé dans la conception d'algorithmes basée sur le paradigme diviser pour régner. Voici un exemple de récursivité avec une fonction de puissance. int Power(int value, int p) { return p != 0 ? value * Power(value, --p) : 1; }

Attention à ne pas dépasser la taille de la pile des exécutions (Sauvegarde des appels de fonctions). En électronique embarquée, la récursivité est souvent proscrite ! L'utilisation de la pile restant trop imprévisible.

SVG Minifier

Les éditeurs graphiques vectoriels tels qu'Adobe Illustrator ou Inkscape incorporent de nombreuses informations dans un fichier SVG qui ne sont pas requises pour la présentation. SVG Minifier supprime ces informations superflues, réduisant ainsi la taille de vos fichiers SVG.

Algorithme de Boruvka (1926)

L'Algorithme de Borůvka a été publié pour la première fois en 1926 par Otakar Borůvka en tant que méthode de construction d’un réseau d’électricité efficace pour la Moravie.

1️⃣️	On parcours chaque points en gardant la branche de poids faible (la plus petite valeur).
2️⃣️	On forme des groupes (points reliées entres eux) et on les relies avec la branche de poids faible.

En algorithmique, on parle de chercher un "arbre couvrant minimum".

Algorithmes similaires : Algorithme de Kruskal - Algorithme de Prim.