Grace HOPPER

	Grace Hoper (9 décembre 1906 - 1er janvier 1992). Elle étudie les mathématiques, la physique et l'économie au Vassar College, et en sort diplômée en 1928. En 1934, elle obtient un doctorat en mathématiques de l'université Yale.
	À partir de 1957, elle travaille pour IBM, où elle défend l'idée qu'un programme devrait pouvoir être écrit dans un langage proche de l'anglais plutôt que d'être calqué sur le langage machine, comme l'assembleur. De cette idée naît le langage COBOL en 1959. Wikipedia	Grace Hopper au clavier de l'UNIVAC, vers 1960.

IA, comment fonctionnes-tu ?

Belle vulgarisation pour comprendre les mécanismes des nouveaux algorithmes d'intelligence artificielle.
Apprentissage automatique - Apprentissage profond 

Steve WOZNIAK

	Stephen Gary Wozniak (11 août 1950) aussi appelé Woz, est un informaticien, professeur d'informatique et électronicien américain. Il est cofondateur de la société Apple Computer avec Steve Jobs et Ronald Wayne, et concepteur des premiers Apple, et est un des pionniers de l'industrie micro-informatique.
	Steve Wozniak fait la connaissance de Steve Jobs en 1970 grâce à son voisin Bill Fernandez, alors camarade de classe de Jobs à la Homestead High School. Ils partagent la même passion de l'électronique, ils deviennent amis et réalisent ensemble de nombreux canulars. Wikipédia	Apple I

Margaret HEAFIELD HAMILTON

	Margaret Heafield Hamilton, née Heafield le 17 août 1936, est une informaticienne, ingénieure système et chef d'entreprise américaine. Elle était directrice du département génie logiciel (« software engineering », terme de son invention) au sein du MIT Instrumentation Laboratory qui conçut le système embarqué du programme spatial Apollo.
	Sur la photo de gauche, Margaret Hamilton se tenant auprès du code du logiciel de navigation qu'elle et son équipe du MIT Draper Lab ont produit pour le programme Apollo. Sur la photo de droite, Margaret Hamilton durant le programme Apollo. Wikipédia

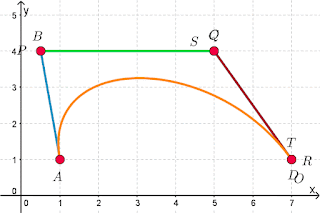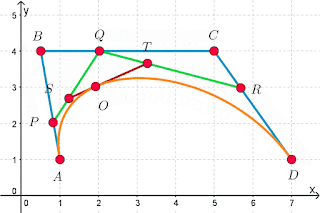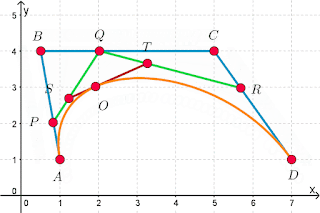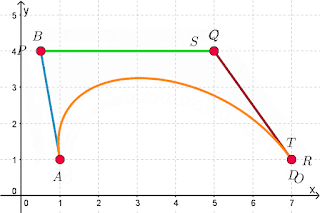
Pierre BÉZIER

Pierre BÉZIER, (1er septembre 1910 - 25 novembre 1999) est un ingénieur en mécanique et en électricité français. Alors que l'automobile est en pleine révolution informatique, il fallait trouver un moyen de stocker les informations de courbures des modélisations. Avec seulement 3 ou 4 points (quadratic ou cubic) vous pouvez dessiner n'importe quelle courbe. De +, cette technique bénéficie d'une excellente ergonomie de saisie. C'est pour cela que les courbes de Bézier sont couramment utilisées dans les fichiers dit "vectoriels" (SVG pour le plus connu). Wikipédia

Ada LOVELACE

	Le 10 décembre 1815 naissait Ada Byron, plus connue de nos jours en tant que Ada Lovelace.
	Même si son rôle exact est sujet à débat, elle est considérée par beaucoup comme la première programmeuse de l'Histoire, grâce à sa contribution aux travaux de Charles Babbage, considéré lui comme le père de l'informatique. Le langage de programmation ADA, créé au début des années 80, a été nommé en son honneur. Wikipédia

La vie d'Ada Lovelace en Lego, par Scilabus - Version Anglaise

Otakar BORUVKA

Otakar Borůvka (10 mai 1899 - 22 juillet 1995) est un mathématicien tchèque connu pour ses contributions à la théorie des graphes publiées longtemps avant qu'elle se soit émancipée comme une discipline mathématique ou informatique. Il est surtout connu pour l'article "O jistém problému minimálním" (Sur un certain problème minimal) publié en 1926, dans lequel il décrit un algorithme de recherche d'arbre couvrant de poids minimal désormais nommé algorithme de Borůvka. Wikipédia

Edsger WYBE DIJKSTRA

	Edsger Wybe Dijkstra (11 mai 1930 - 6 août 2002) est un mathématicien et informaticien néerlandais du xxe siècle. Il reçoit en 1972 le prix Turing pour ses contributions sur la science et l’art des langages de programmation et au langage Algol.
	Il est à l'origine de l'algorithme éponyme, l'algorithme de Dijkstra, permettant de calculer des plus courts chemins dans un graphe orienté. Wikipédia

Joseph KRUSKAL

Joseph Kruskal (29 janvier 1928 - 19 septembre 2010) est un mathématicien, statisticien, chercheur en informatique et psychométricien américain. En informatique, sa découverte la plus connue est l’algorithme de Kruskal pour la détermination de l’arbre couvrant de poids minimal (ARM) dans les graphes pondérés. Wikipédia

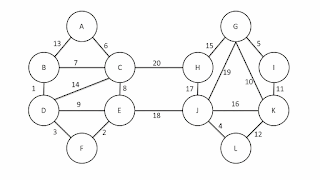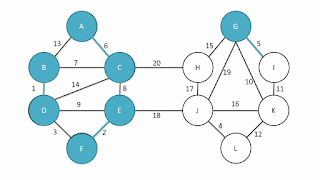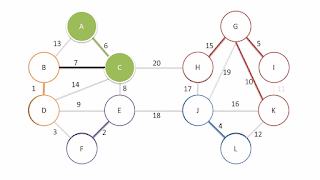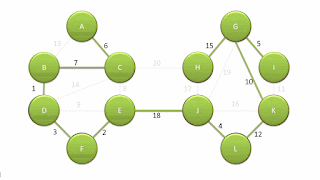
Algorithme de Kruskal (1956)

L'Algorithme de Kruskal est apparu pour la première fois dans les Actes de l’"American Mathematical Society", pages 48 à 50 en 1956, et a été écrit par Joseph Kruskal. Il consiste à trouver l'arbre couvrant minimum. 1️⃣️ On cherche la distance la plus courte entre 2 points. 2️⃣️ Si un autre chemin existe déjà, on ne retient pas cette branche. 3️⃣️ On répète l'étape 1 jusqu'à ce que tous les points soient accessibles par n'importe quel autres points. Cet algorithme, très simple à coder, peut se révéler très consommateur de calculs lors du classement des différentes routes suivant leur distance et de la vérification de routes existantes (Algorithme de parcours en largeur ou profondeur). Algorithmes similaires : Algorithme de Borůvka - Algorithme de Prim.

Marche de Jarvis

L'algorithme Marche de Jarvis consiste à trouver le polygone convexe (enveloppe) regroupant tous les points. 1️⃣️ On part du point P0 d’abscisse minimum. 2️⃣️ On cherche le point suivant Ps : Angle minimum formé par (P0-Ps) et la demi-droite verticale partant de P0. 3️⃣️ On répète l'opération jusqu'à retomber sur le point de départ P0. Cette méthode peut considérablement être améliorée en performance avec des techniques dites Diviser pour régner (Divide-and-conquer algorithm).

Détecter si un point est à l'intérieur d'un polygone convexe

Explications sur un polygone convexe On vérifie que le point est toujours à gauche (résultat négatif du déterminant si l'on parcourt le polygone dans le sens radial) de chacune des droites formées par les arrêtes. Cet algorithme est bien plus performant que ceux donnés sur les liens ci-dessous, et plus pratique car nous pouvons facilement savoir si un point est sur une arrête (D = 0 -> 1 fois) ou un sommet (D = 0 -> 2 fois)

https://www.geeksforgeeks.org/how-to-check-if-a-given-point-lies-inside-a-polygon/
https://www.geeksforgeeks.org/check-whether-a-given-point-lies-inside-a-triangle-or-not/